maximum-weight-matching/doc/Algorithm.md

Implementation of Maximum Weighted Matching

Introduction

This document describes the implementation of an algorithm that computes a maximum weight matching in a general graph in time O(n (n + m) log n), where n is the number of vertices in the graph and m is the number of edges.

In graph theory, a matching is a subset of edges such that none of them share a common vertex.

A maximum cardinality matching is a matching that contains the largest possible number of edges (or equivalently, the largest possible number of vertices).

If a graph has weights assigned to its edges, a maximum weight matching is a matching that achieves the largest possible sum of weights of matched edges. An algorithm for maximum weight matching can obviously also be used to calculate a maximum cardinality matching by simply assigning weight 1 to all edges.

Certain related problems can be understood as restrictions of maximum weighted matching in general graphs. Examples are: maximum matching in bipartite graphs, maximum cardinality matching in general graphs, and maximum weighted matching in general graphs with edge weights limited to integers in a certain range. Clearly, an algorithm for maximum weighted matching in general graphs also solves all of these restricted problems. However, some of the restricted problems can be solved with algorithms that are simpler and/or faster than the known algorithms for the general problem. The rest of this document does not consider restricted problems. My focus is purely on maximum weighted matching in general graphs.

In this document, n refers to the number of vertices and m refers to the number of edges in the graph.

A timeline of matching algorithms

In 1963, Jack Edmonds published the first polynomial-time algorithm for maximum matching in general graphs [1] [2] . Efficient algorithms for bipartite graphs were already known at the time, but generalizations to non-bipartite graphs would tend to require an exponential number of steps. Edmonds solved this by explicitly detecting blossoms (odd-length alternating cycles) and adding special treatment for them. He also introduced a linear programming technique to handle weighted matching. The resulting maximum weighted matching algorithm runs in time O(n⁴).

In 1973, Harold N. Gabow published a maximum weighted matching algorithm that runs in time O(n³) [3] . It is based on the ideas of Edmonds, but uses different data structures to reduce the amount of work.

In 1983, Galil, Micali and Gabow published a maximum weighted matching algorithm that runs in time O(n m log n) [4] . It is an implementation of Edmonds' blossom algorithm that uses advanced data structures to speed up critical parts of the algorithm. This algorithm is asymptotically faster than O(n³) for sparse graphs, but slower for highly dense graphs.

In 1983, Zvi Galil published an overview of algorithms for 4 variants of the matching problem [5] : maximum-cardinality resp. maximum-weight matching in bipartite resp. general graphs. I like this paper a lot. It explains the algorithms from first principles and can be understood without prior knowledge of the literature. The paper describes a maximum weighted matching algorithm that is similar to Edmonds' blossom algorithm, but carefully implemented to run in time O(n³). It then sketches how advanced data structures can be added to arrive at the Galil-Micali-Gabow algorithm that runs in time O(n m log n).

In 1990, Gabow published a maximum weighted matching algorithm that runs in time O(n m + n² log n) [6] . It uses several advanced data structures, including Fibonacci heaps. Unfortunately I don't understand this algorithm at all.

Choosing an algorithm

I selected the O(n m log n) algorithm by Galil, Micali and Gabow [4].

This algorithm is asymptotically optimal for sparse graphs. It has also been shown to be quite fast in practice on several types of graphs including random graphs [7].

This algorithm is more difficult to implement than the older O(n³) algorithm. In particular, it requires a specialized data structure to implement mergeable priority queues. This increases the size and complexity of the code quite a bit. However, in my opinion the performance improvement is worth the extra effort.

Description of the algorithm

My implementation roughly follows the description by Zvi Galil in [5] . I recommend reading that paper before diving into my description below. The paper explains the algorithm in depth and shows how it relates to matching in bipartite graphs and non-weighted graphs.

There are subtle aspects to the algorithm that are tricky to implement correctly but are mentioned only briefly in the paper. In this section, I describe the algorithm from my own perspective: a programmer struggling to implement the algorithm correctly.

My goal is only to describe the algorithm, not to prove its correctness.

Basic concepts

An edge-weighted, undirected graph G consists of a set V of n vertices and a set E of m edges.

Vertices are represented by non-negative integers from 0 to n-1: V = { 0, 1, ..., n-1 }

Edges are represented by tuples: E = { (x, y, w), ... }
where the edge (x, y, w) is incident on vertices x and y and has weight w.
The order of vertices is irrelevant, i.e. (x, y, w) and (y, x, w) represent the same edge.
Edge weights may be integers or floating point numbers.
There can be at most one edge between any pair of vertices.
A vertex can not have an edge to itself.

A matching is a subset of edges without any pair of edges sharing a common vertex.
An edge is matched if it is part of the matching, otherwise it is unmatched.
A vertex is matched if it is incident to an edge in the matching, otherwise it is unmatched.

An alternating path is a simple path that alternates between matched and unmatched edges.

Figure 1

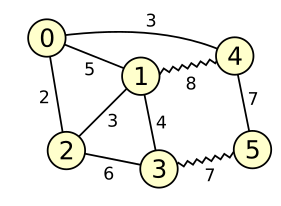
Figure 1 depicts a graph with 6 vertices and 9 edges. Wavy lines represent matched edges; straight lines represent edges that are currently unmatched. The matching has weight 8 + 7 = 15. An example of an alternating path would be 0 - 1 - 4 - 5 - 3 (but there are many others).

Augmenting paths

An augmenting path is an alternating path that begins and ends in two unmatched vertices.

An augmenting path can be used to extend the matching as follows: remove all matched edges on the augmenting path from the matching, and add all previously unmatched edges on the augmenting path to the matching. The result is again a valid matching, and the number of matched edges has increased by one.

The matching in figure 1 above has several augmenting paths. For example, the edge from vertex 0 to vertex 2 is by itself an augmenting path. Augmenting along this path would increase the weight of the matching by 2. Another augmenting path is 0 - 1 - 4 - 5 - 3 - 2, which would increase the weight of the matching by 3. Finally, 0 - 4 - 1 - 2 is also an augmenting path, but it would decrease the weight of the matching by 2.

Main algorithm

Our algorithm to compute a maximum weighted matching is as follows:

• Start with an empty matching (all edges unmatched).
• Repeat the following steps:
  • Find an augmenting path that provides the largest possible increase of the weight of the matching.
  • If there is no augmenting path that increases the weight of the matching, end the algorithm. The current matching is a maximum-weight matching.
  • Otherwise, use the augmenting path to update the matching.
  • Continue by searching for another augmenting path, etc.

This algorithm ends when there are no more augmenting paths that increase the weight of the matching. In some cases, there may still be augmenting paths which do not increase the weight of the matching, implying that the maximum-weight matching has fewer edges than the maximum cardinality matching.

Every iteration of the main loop is called a stage. Note that the final matching contains at most n/2 edges, therefore the algorithm performs at most n/2 stages.

The only remaining challenge is finding an augmenting path. Specifically, finding an augmenting path that increases the weight of the matching as much as possible.

Blossoms

A blossom is an odd-length cycle that alternates between matched and unmatched edges. Such cycles complicate the search for augmenting paths. To overcome these problems, blossoms must be treated specially. The trick is to temporarily replace the vertices and edges that are part of the blossom by a single super-vertex. This is called shrinking the blossom. The search for an augmenting path then continues in the modified graph in which the odd-length cycle no longer exists. It may later become necessary to expand the blossom (undo the shrinking step).

For example, the cycle 0 - 1 - 4 - 0 in figure 1 above is an odd-length alternating cycle, and therefore a candidate to become a blossom.

In practice, we do not remove vertices or edges from the graph while shrinking a blossom. Instead the graph is left unchanged, but a separate data structure keeps track of blossoms and which vertices are contained in which blossoms.

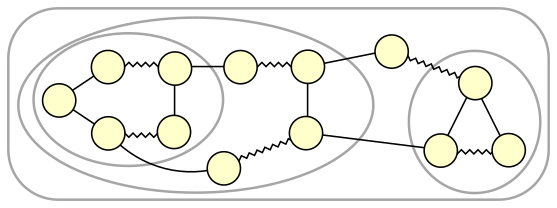
A graph can contain many blossoms. Furthermore, after shrinking a blossom, that blossom can become a sub-blossom in a bigger blossom. Figure 2 depicts a graph with several nested blossoms.

Figure 2: Nested blossoms

To describe the algorithm unambiguously, we need precise definitions:

• A blossom is either a single vertex, or an odd-length alternating cycle of sub-blossoms.
• A non-trivial blossom is a blossom that is not a single vertex.
• A top-level blossom is a blossom that is not contained inside another blossom. It can also be a single vertex which is not part of any blossom.
• The base vertex of a blossom is the only vertex in the blossom that is not matched to another vertex in the same blossom. The base vertex is either unmatched, or matched to a vertex outside the blossom. In a single-vertex blossom, its only vertex is the base vertex. In a non-trivial blossom, the base vertex is equal to the base vertex of the unique sub-blossom that begins and ends the alternating cycle.
• The parent of a non-top-level blossom is the directly enclosing blossom in which it occurs as a sub-blossom. Top-level blossoms do not have parents.

Non-trivial blossoms are created by shrinking and destroyed by expanding. These are explicit steps of the algorithm. This implies that not every odd-length alternating cycle is a blossom. The algorithm decides which cycles are blossoms.

Just before a new blossom is created, its sub-blossoms are initially top-level blossoms. After creating the blossom, the sub-blossoms are no longer top-level blossoms because they are contained inside the new blossom, which is now a top-level blossom.

Every vertex is contained in precisely one top-level blossom. This may be either a trivial blossom which contains only that single vertex, or a non-trivial blossom into which the vertex has been absorbed through shrinking. A vertex may belong to different top-level blossoms over time as blossoms are created and destroyed by the algorithm. I use the notation B(x) to indicate the top-level blossom that contains vertex x.

Searching for an augmenting path

Recall that the matching algorithm repeatedly searches for an augmenting path that increases the weight of the matching as much as possible. I'm going to postpone the part that deals with "increasing the weight as much as possible". For now, all we need to know is this: At a given step in the algorithm, some edges in the graph are tight while other edges have slack. An augmenting path that consists only of tight edges is guaranteed to increase the weight of the matching as much as possible.

While searching for an augmenting path, we simply restrict the search to tight edges, ignoring all edges that have slack. Certain explicit actions of the algorithm cause edges to become tight or slack. How this works will be explained later.

To find an augmenting path, the algorithm searches for alternating paths that start in an unmatched vertex. The collection of such alternating paths forms a forest of trees. Each tree is rooted in an unmatched vertex, and all paths from the root to the leaves of a tree are alternating paths. The nodes in these trees are top-level blossoms.

To facilitate the search, top-level blossoms are labeled as either S or T or unlabeled. Label S is assigned to the roots of the alternating trees, and to nodes at even distance from the root. Label T is assigned to nodes at odd distance from the root of an alternating tree. Unlabeled blossoms are not (yet) part of an alternating tree. (In some papers, the label S is called outer and T is called inner.)

It is important to understand that labels S and T are assigned only to top-level blossoms, not to individual vertices. However, it is often relevant to know the label of the top-level blossom that contains a given vertex. I use the following terms for convenience:

• an S-blossom is a top-level blossom with label S;
• a T-blossom is a top-level blossom with label T;
• an S-vertex is a vertex inside an S-blossom;
• a T-vertex is a vertex inside a T-blossom.

Edges that span between two S-blossoms are special. If both S-blossoms are part of the same alternating tree, the edge is part of an odd-length alternating cycle. The lowest common ancestor node in the alternating tree forms the beginning and end of the alternating cycle. In this case a new blossom must be created by shrinking the cycle. If the two S-blossoms are in different alternating trees, the edge that links the blossoms is part of an augmenting path between the roots of the two trees.

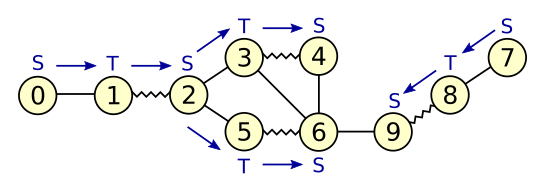
Figure 3: Growing alternating trees

The graph in figure 3 contains two unmatched vertices: 0 and 7. Both form the root of an alternating tree. Blue arrows indicate edges in the alternating trees, pointing away from the root. The graph edge between vertices 4 and 6 connects two S-blossoms in the same alternating tree. Scanning this edge will cause the creation of a new blossom with base vertex 2. The graph edge between vertices 6 and 9 connects two S-blossoms which are part of different alternating trees. Scanning this edge will discover an augmenting path between vertices 0 and 7.

Note that all vertices in the graph of figure 3 happen to be top-level blossoms. In general, the graph may already contain non-trivial blossoms. Alternating trees are constructed over top-level blossoms, not necessarily over individual vertices.

When a vertex becomes an S-vertex, it is added to a queue. The search procedure considers these vertices one-by-one and tries to use them to either grow the alternating tree (thus adding new vertices to the queue), or discover an augmenting path or a new blossom.

The search for an augmenting path proceeds as follows:

• Mark all top-level blossoms as unlabeled.
• Initialize an empty queue Q.
• Assign label S to all top-level blossoms that contain an unmatched vertex. Add all vertices inside such blossoms to Q.
• Repeat until Q is empty:
  • Take a vertex x from Q.
  • Scan all tight edges (x, y, w) that are incident on vertex x.
    • Find the top-level blossom B(x) that contains vertex x and the top-level blossom B(y) that contains vertex y.
    • If B(x) and B(y) are the same blossom, ignore this edge. (It is an internal edge in the blossom.)
    • Otherwise, if blossom B(y) is unlabeled, assign label T to it. The base vertex of B(y) is matched (otherwise B(y) would have label S). Find the vertex t which is matched to the base vertex of B(y) and find its top-level blossom B(t) (this blossom is still unlabeled). Assign label S to blossom B(t), and add all vertices inside B(t) to Q.
    • Otherwise, if blossom B(y) has label T, ignore this edge.
    • Otherwise, if blossom B(y) has label S, there are two scenarios:
      • Either B(x) and B(y) are part of the same alternating tree. In that case, we have discovered an odd-length alternating cycle. Shrink the cycle into a blossom and assign label S to it. Add all vertices inside its T-labeled sub-blossoms to Q. (Vertices inside S-labeled sub-blossoms have already been added to Q and must not be added again.) Continue the search for an augmenting path.
      • Otherwise, if B(x) and B(y) are part of different alternating trees, we have found an augmenting path between the roots of those trees. End the search and return the augmenting path.
• If Q becomes empty before an augmenting path has been found, it means that no augmenting path exists (which consists of only tight edges).

For each top-level blossom, we keep track of its label as well as the edge through which it obtained its label (attaching it to the alternating tree). These edges are needed to trace back through the alternating tree to construct a blossom or an alternating path.

When an edge between S-blossoms is discovered, it is handled as follows:

• The two top-level blossoms are B(x) and B(y), both labeled S.
• Trace up through the alternating trees from B(x) and B(y) towards the root.
• If the blossoms are part of the same alternating tree, the tracing process eventually reaches a lowest common ancestor of B(x) and B(y). In that case a new blossom must be created. Its alternating cycle starts at the common ancestor, follows the path through the alternating tree down to B(x), then via the scanned edge to B(y), then through the alternating tree up to the common ancestor. (Note it is possible that either B(x) or B(y) is itself the lowest common ancestor.)
• Otherwise, the blossoms are in different trees. The tracing process will eventually reach the roots of both trees. At that point we have traced out an augmenting path between the two roots.

Note that the matching algorithm uses two different types of tree data structures. These two types of trees are separate concepts. But since they are both trees, there is potential for accidentally confusing them. It may be helpful to explicitly distinguish the two types:

• A forest of blossom structure trees represents the nested structure of blossoms. Every node in these trees is a blossom. The roots are the top-level blossoms. The leaf nodes are the single vertices. The child nodes of each non-leaf node represent its sub-blossoms. Every vertex is a leaf node in precisely one blossom structure tree. A blossom structure tree may consist of just one single node, representing a vertex that is not part of any non-trivial blossom.
• A forest of alternating trees represents an intermediate state during the search for an augmenting path. Every node in these trees is a top-level blossom. The roots are top-level blossoms with an unmatched base vertex. Every labeled top-level blossom is part of an alternating tree. Unlabeled blossoms are not (yet) part of a tree.

Augmenting the matching

Once an augmenting path has been found, augmenting the matching is relatively easy. Simply follow the path, adding previously unmatched edges to the matching and removing previously matched edges from the matching.

A useful data structure to keep track of matched edges is an array mate[x] indexed by vertex. If vertex x is matched, mate[x] contains the index of the vertex to which it is matched. If vertex x is unmatched, mate[x] contains -1.

A slight complication arises when the augmenting path contains a non-trivial blossom. The search returns an augmenting path over top-level blossoms, without details about the layout of the path within blossoms. Any parts of the path that run through a blossom must be traced in order to update the matched/unmatched status of the edges in the blossom.

When an augmenting path runs through a blossom, it always runs between the base vertex of the blossom and some sub-blossom (potentially the same sub-blossom that contains the base vertex). If the base vertex is unmatched, it forms the start or end of the augmenting path. Otherwise, the augmenting path enters the blossom though the matched edge of the base vertex. From the opposite direction, the augmenting path enters the blossom through an unmatched edge. It follows that the augmenting path must run through an even number of internal edges of the blossom. Fortunately, every sub-blossom can be reached from the base through an even number of steps by walking around the blossom in the appropriate direction.

Augmenting along a path through a blossom causes a reorientation of the blossom. Afterwards, it is still a blossom and still consists of an odd-length alternating cycle, but the cycle begins and ends in a different sub-blossom. The blossom also has a different base vertex. (In specific cases where the augmenting path merely "grazes" a blossom, the orientation and base vertex remain unchanged.)

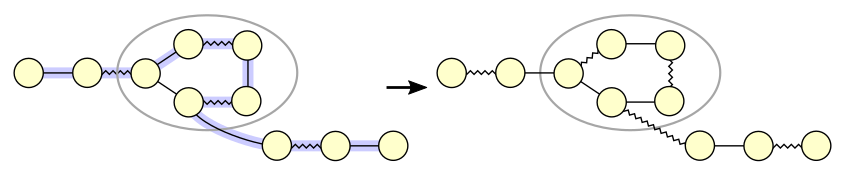
Figure 4: Augmenting path through a blossom

Figure 4 shows an augmenting path that runs through a blossom. The augmenting path runs through an even number of internal edges in the blossom, which in this case is not the shortest way around the blossom. After augmenting, the blossom has become reoriented: a different vertex became the base vertex.

In case of nested blossoms, non-trivial sub-blossoms on the augmenting path must be updated recursively.

Note that the process of repeatedly augmenting the matching will never cause a matched vertex to become unmatched. Once a vertex is matched, augmenting may cause the vertex to become matched to a different vertex, but it can not cause the vertex to become unmatched.

Edge slack and dual variables

We still need a method to determine which edges are tight. This is done by means of so-called dual variables.

The purpose of dual variables can be explained by rephrasing the maximum matching problem as an instance of linear programming. I'm not going to do that here. I will describe how the algorithm uses dual variables without explaining why. For the mathematical background, I recommend reading [5] .

Every vertex x has a dual variable u_x. Furthermore, every non-trivial blossom B has a dual variable z_B. These variables contain non-negative numbers which change over time through actions of the algorithm.

Every edge in the graph imposes a constraint on the dual variables: The weight of the edge between vertices x and y must be less or equal to the sum of the dual variables u_x plus u_y plus all z_B of blossoms B that contain the edge. (A blossom contains an edge if it contains both incident vertices.) This constraint is more clearly expressed in a formula:

 u_x + u_y + \sum_{(x,y) \in B} z_B \ge w_{x,y} 

The slack π_x,y of the edge between vertices x and y is a non-negative number that indicates how much room is left before the edge constraint would be violated:

 \pi_{x,y} = u_x + u_y + \sum_{(x,y) \in B} z_B - w_{x,y} 

An edge is tight if and only if its slack is zero. Given the values of the dual variables, it is very easy to calculate the slack of an edge which is not contained in any blossom: simply add the duals of its incident vertices and subtract the weight. To check whether an edge is tight, simply compute its slack and check whether it is zero.

Calculating the slack of an edge that is contained in one or more blossoms is a little tricky, but fortunately we don't need such calculations. The search for augmenting paths only considers edges that span between top-level blossoms, not edges that are contained inside blossoms. So we never need to check the tightness of internal edges in blossoms.

A matching has maximum weight if it satisfies all of the following constraints:

• All dual variables and edge slacks are non-negative: u_i ≥ 0 , z_B ≥ 0 , π_x,y ≥ 0
• All matched edges have zero slack: edge (x, y) matched implies π_x,y = 0
• All unmatched vertices have dual variable zero: vertex x unmatched implies u_x = 0

The first two constraints are satisfied at all times while the matching algorithm runs. When the algorithm updates dual variables, it ensures that dual variables and edge slacks remain non-negative. It also ensures that matched edges remain tight, and that edges which are part of the odd-length cycle in a blossom remain tight. When the algorithm augments the matching, it uses an augmenting path that consists of only tight edges, thus ensuring that newly matched edges have zero slack.

The third constraint is initially not satisfied. The algorithm makes progress towards satisfying this constraint in two ways: by augmenting the matching, thus reducing the number of unmatched vertices, and by reducing the value of the dual variables of unmatched vertices. Eventually, either all vertices are matched or all unmatched vertices have zero dual. At that point the maximum weight matching has been found.

When the matching algorithm is finished, the constraints can be checked to verify that the matching is optimal. This check is simpler and faster than the matching algorithm itself. It can therefore be a useful way to guard against bugs in the matching algorithm.

Rules for updating dual variables

At the start of the matching algorithm, all vertex dual variables u_i are initialized to the same value: half of the greatest edge weight value that occurs on any edge in the graph.

 u_i = {1 \over 2} \cdot \max_{(x,y) \in E} w_{x,y} 

Initially, there are no blossoms yet so there are no z_B to be initialized. When the algorithm creates a new blossom, it initializes its dual variable to z_B = 0. Note that this does not change the slack of any edge.

If a search for an augmenting path fails while there are still unmatched vertices with positive dual variables, it may not yet have found the maximum weight matching. In such cases the algorithm updates the dual variables until either an augmenting path gets unlocked or the dual variables of all unmatched vertices reach zero.

To update the dual variables, the algorithm chooses a value δ that represents how much the duals will change. It then changes dual variables as follows:

• u_x ← u_x − δ for every S-vertex x
• u_x ← u_x + δ for every T-vertex x
• z_B ← z_B + 2 * δ for every non-trivial S-blossom B
• z_B ← z_B − 2 * δ for every non-trivial T-blossom B

Dual variables of unlabeled blossoms and their vertices remain unchanged. Dual variables z_B of non-trivial sub-blossoms also remain changed; only top-level blossoms have their z_B updated.

Note that these rules ensure that no change occurs to the slack of any edge which is matched, or part of an alternating tree, or contained in a blossom. Such edges are tight and remain tight through the update. However, the update reduces the slack of edges between S blossoms and edges between S-blossoms and unlabeled blossoms. It may cause some of these edges to become tight, allowing them to be used to construct an augmenting path.

The value of δ is determined as follows: δ = min(δ₁, δ₂, δ₃, δ₄) where

• δ₁ is the minimum u_x of any S-vertex x.
• δ₂ is the minimum slack of any edge between an S-blossom and an unlabeled blossom.
• δ₃ is half of the minimum slack of any edge between two different S-blossoms.
• δ₄ is half of the minimum z_B of any T-blossom B.

δ₁ protects against any vertex dual becoming negative. δ₂ and δ₃ together protect against any edge slack becoming negative. δ₄ protects against any blossom dual becoming negative.

If the dual update is limited by δ₁, it causes the duals of all remaining unmatched vertices to become zero. At that point the maximum matching has been found and the algorithm ends. If the dual update is limited by δ₂ or δ₃, it causes an edge to become tight. The next step is to either add that edge to the alternating tree (δ₂) or use it to construct a blossom or augmenting path (δ₃). If the dual update is limited by δ₄, it causes the dual variable of a T-blossom to become zero. The next step is to expand that blossom.

Discovering tight edges through delta steps

A delta step may find that δ = 0, implying that the dual variables don't change. This can still be useful since all types of updates have side effects (adding an edge to an alternating tree, or expanding a blossom) that allow the algorithm to make progress. In fact, it is convenient to let the dual update mechanism drive the entire process of discovering tight edges and growing alternating trees.

In my description of the search algorithm above, I stated that a tight edge between a newly labeled S-vertex and an unlabeled vertex or a different S-blossom should be used to grow the alternating tree or to create a new blossom or to form an augmenting path. However, it turns out to be easier to postpone the use of such edges until the next delta step. While scanning newly labeled S-vertices, edges to unlabeled vertices or different S-blossoms are discovered but not yet used. Such edges will merely be indexed in a suitable data structure. Even if the edge is tight, it will be indexed rather than used right away.

Once the scan completes, a delta step will be done. If any tight edges were discovered during the scan, the delta step will find that either δ₂ = 0 or δ₃ = 0. The corresponding step (growing the alternating tree, creating a blossom or augmenting the matching) will occur at that point. If no suitable tight edges exist, a real change of dual variables will occur.

The search for an augmenting path becomes as follows:

• Mark all top-level blossoms as unlabeled.
• Initialize an empty queue Q.
• Assign label S to all top-level blossoms that contain an unmatched vertex. Add all vertices inside such blossoms to Q.
• Repeat until either an augmenting path is found or δ₁ = 0:
  • Scan all vertices in Q as described earlier. Build an index of edges to unlabeled vertices or other S-blossoms. Do not yet use such edges to change the alternating tree, even if the edge is tight.
  • Calculate δ and update dual variables as described above.
  • If δ = δ₁, end the search. The maximum weight matching has been found.
  • If δ = δ₂, use the corresponding edge to grow the alternating tree. Assign label T to the unlabeled blossom. Then assign label S to its mate and add the new S-vertices to Q.
  • If δ = δ₃ and the corresponding edge connects two S-blossoms in the same alternating tree, use the edge to create a new blossom. Add the new S-vertices to Q.
  • If δ = δ₃ and the corresponding edge connects two S-blossoms in different alternating trees, use the edge to construct an augmenting path. End the search and return the augmenting path.
  • If δ = δ₄, expand the corresponding T-blossom.

It may seem complicated, but this is actually easier. The code that scans newly labeled S-vertices, no longer needs to treat tight edges specially.

In general, multiple updates of the dual variables are necessary during a single stage of the algorithm. Remember that a stage is the process of growing alternating trees until an augmenting path is found. A stage ends either by augmenting the matching, or by concluding that no further improvement is possible.

Expanding a blossom

There are two scenarios where a blossom must be expanded. One is when the dual variable of a T-blossom becomes zero after a dual update limited by δ₄. In this case the blossom must be expanded, otherwise further dual updates would cause its dual to become negative.

The other scenario is when the algorithm is about to assign label T to an unlabeled blossom with dual variable zero. A T-blossom with zero dual serves no purpose, potentially blocks an augmenting path, and is likely to be expanded anyway via a δ₄=0 update. It is therefore better to preemptively expand the unlabeled blossom. The step that would have assigned label T to the blossom is then re-evaluated, which will cause it to assign label T to a sub-blossom of the expanded blossom. It may then turn out that this sub-blossom must also be expanded, and this becomes a recursive process until we get to a sub-blossom that is either a single vertex or a blossom with non-zero dual.

Note that [5] specifies that all top-level blossoms with dual variable zero should be expanded after augmenting the matching. This prevents the existence of unlabeled top-level blossoms with zero dual, and therefore prevents the scenario where label T would be assigned to such blossoms. That strategy is definitely correct, but it may lead to unnecessary expanding of blossoms which are then recreated during the search for the next augmenting path. Postponing the expansion of these blossoms until they are about to be labeled T, as described above, may be faster in some cases.

Expanding an unlabeled top-level blossom B is pretty straightforward. Simply promote all of its sub-blossoms to top-level blossoms, then delete B. Note that the slack of all edges remains unchanged, since z_B = 0.

Expanding a T-blossom is tricky because the labeled blossom is part of an alternating tree. After expanding the blossom, the part of the alternating tree that runs through the blossom must be reconstructed. An alternating path through a blossom always runs through its base vertex. After expanding T-blossom B, we can reconstruct the alternating path by following it from the sub-blossom where the path enters B to the sub-blossom that contains the base vertex (choosing the direction around the blossom that takes an even number of steps). We then assign alternating labels T and S to the sub-blossoms along that path and link them into the alternating tree. All vertices of sub-blossoms that got label S are inserted into Q.

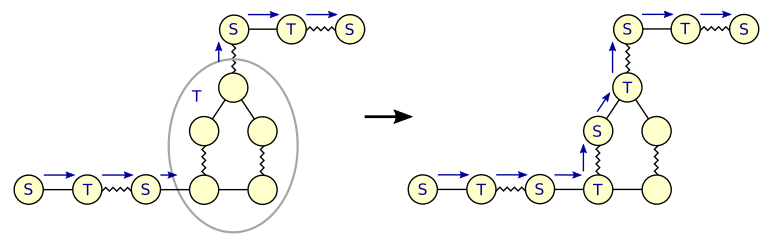
Figure 5: Expanding a T-blossom

Keeping track of the top-level blossom of each vertex

The algorithm often needs to find the top-level blossom B(x) that contains a given vertex x.

A naive implementation may keep this information is an array where the element with index x holds a pointer to blossom B(x). Lookup in this array would be fast, but keeping the array up-to-date takes too much time. There can be O(n) stages, and O(n) blossoms can be created or expanded during a stage, and a blossom can contain O(n) vertices, therefore the total number of updates to the array could add up to O(n³).

To solve this, we use a special data structure: a concatenable priority queue. Each top-level blossom maintains an instance of this type of queue, containing its vertices. Each vertex is a member in precisely one such queue.

To find the top-level blossom B(x) that contains a given vertex x, we determine the queue instance in which the vertex is a member. This takes time O(log n). The queue instance corresponds directly to a specific blossom, which we can find for example by storing a pointer to the blossom inside the queue instance.

When a new blossom is created, the concatenable queues of its sub-blossoms are merged to form one concatenable queue for the new blossom. Concatenating two queues produces a new queue that contains all members of the original queues. This operation takes time O(log n). To merge the queues of k sub-blossoms, the concatenation step is repeated k-1 times, taking total time O(k log n).

When a blossom is expanded, its concatenable queue is un-concatenated to recover separate queues for the sub-blossoms. This also takes time O(log n) for each sub-blossom.

Implementation details of a concatenable queue will be discussed later in this document.

Lazy updating of dual variables

During a delta step, the dual variables of labeled vertices and blossoms change as described above. Updating these variables directly would take time O(n) per delta step. The total number of delta steps during a matching may be Θ(n²), pushing the total time to update dual variables to O(n³) which is too slow.

To solve this, [4] describes a technique that stores dual values in a modified form which is invariant under delta steps. The modified values can be converted back to the true dual values when necessary. [7] describes a slightly different technique which I find easier to understand. My implementation is very similar to theirs.

The first trick is to keep track of the running sum of δ values since the beginning of the algorithm. Let's call that number Δ. At the start of the algorithm Δ = 0, but the value increases as the algorithm goes through delta steps.

For each non-trivial blossom, rather than storing its true dual value, we store a modified dual value:

• For an S-blossom, the modified dual value is z'_B = z_B - 2 Δ
• For a T-blossom, the modified dual value is z'_B = z_B + 2 Δ
• For an unlabeled blossom or non-top-level blossom, the modified dual value is equal to the true dual value.

These modified values are invariant under delta steps. Thus, there is no need to update the stored values during a delta step.

Since the modified blossom dual value depends on the label (S or T) of the blossom, the modified value must be updated whenever the label of the blossom changes. This update can be done in constant time, and changing the label of a blossom is in any case an explicit step, so this won't increase the asymptotic run time.

For each vertex, rather than storing its true dual value, we store a modified dual value:

• For an S-vertex, the modified dual value is u'_x = u_x + Δ
• For a T-vertex, the modified dual value is u'_x = u_x - offset_B(x) - Δ
• For an unlabeled vertex, the modified dual value is u'_x = u_x - offset_B(x)

where offset_B is an extra variable which is maintained for each top-level blossom.

Again, the modified values are invariant under delta steps, which implies that no update to the stored values is necessary during a delta step.

Since the modified vertex dual value depends on the label (S or T) of its top-level blossom, an update is necessary when that label changes. For S-vertices, we can afford to apply that update directly to the vertices involved. This is possible since a vertex becomes an S-vertex at most once per stage.

The situation is more complicated for T-vertices. During a stage, a T-vertex can become unlabeled if it is part of a T-blossom that gets expanded. The same vertex can again become a T-vertex, then again become unlabeled during a subsequent blossom expansion. In this way, a vertex can transition between T-vertex and unlabeled vertex up to O(n) times within a stage. We can not afford to update the stored modified vertex dual so many times. This is where the offset variables come in. If a blossom becomes a T-blossom, rather than updating the modified duals of all vertices, we update only the offset variable of the blossom such that the modified vertex duals remain unchanged. If a blossom is expanded, we push the offset values down to its sub-blossoms.

Efficiently computing δ

To perform a delta step, the algorithm computes the values of δ₁, δ₂, δ₃ and δ₄ and determines which edge (δ₂, δ₃) or blossom (δ₄) achieves the minimum value.

A naive implementation might compute δ by looping over the vertices, blossoms and edges in the graph. The total number of delta steps during a matching may be Θ(n²), pushing the total time for δ calculations to O(n² m) which is much too slow. [4] introduces a combination of data structures from which the value of δ can be computed efficiently.

δ₁ is the minimum dual value of any S-vertex. This value can be computed in constant time. The dual value of an unmatched vertex is reduced by δ during every delta step. Since all vertex duals start with the same dual value u_start, all unmatched vertices have dual value u_start - Δ, which is the minimum dual value among all vertices.

δ₃ is half of the minimum slack of any edge between two different S-blossoms. To compute this efficiently, we keep edges between S-blossoms in a priority queue. The edges are inserted into the queue during scanning of newly labeled S-vertices. To compute δ₃, we simply find the minimum-priority element of the queue.

A complication may occur when a new blossom is created. Edges that connect different top-level S-blossoms before creation of the new blossom, may end up as internal edges inside the newly created blossom. This implies that such edges would have to be removed from the δ₃ priority queue, but that would be quite difficult. Instead, we just let those edges stay in the queue. When computing the value of δ₃, we thus have to check whether the minimum element represents an edge between different top-level blossoms. If not, we discard such stale elements until we find an edge that does.

A complication occurs when dual variables are updated. At that point, the slack of any edge between different S-blossoms decreases by 2*δ. But we can not afford to update the priorities of all elements in the queue. To solve this, we set the priority of each edge to its modified slack.

The modified slack of an edge is defined as follows:

 \pi'_{x,y} = u'_x + u'_y - w_{x,y} 

The modified slack is computed in the same way as true slack, except it uses the modified vertex duals instead of true vertex duals. Blossom duals are ignored since we will never compute the modified slack of an edge that is contained inside a blossom.

Because modified vertex duals are invariant under delta steps, so is the modified edge slack. As a result, the priorities of edges in the priority queue remain unchanged during a delta step.

δ₄ is half of the minimum dual variable of any T-blossom. To compute this efficiently, we keep non-trivial T-blossoms in a priority queue. The blossoms are inserted into the queue when they become a T-blossom and removed from the queue when they stop being a T-blossom.

A complication occurs when dual variables are updated. At that point, the dual variable of any T-blossom decreases by 2*δ. But we can not afford to update the priorities of all elements in the queue. To solve this, we set the priority of each blossom to its modified dual value z'_B = z_B + 2*Δ. These values are invariant under delta steps.

δ₂ is the minimum slack of any edge between an S-vertex and unlabeled vertex. To compute this efficiently, we use a fairly complicated strategy that involves three levels of priority queues.

At the lowest level, every T-vertex or unlabeled vertex maintains a separate priority queue of edges between itself and any S-vertex. Edges are inserted into this queue during scanning of newly labeled S-vertices. Note that S-vertices do not maintain this type of queue.

The priorities of edges in these queues are set to their modified slack. This ensures that the priorities remain unchanged during delta steps. The priorities also remain unchanged when the T-vertex becomes unlabeled or the unlabeled vertex becomes a T-vertex.

At the middle level, every T-blossom or unlabeled top-level maintains a priority queue containing its vertices. This is in fact the concatenable priority queue instance that is maintained by every top-level blossom as described earlier in this document. The priority of each vertex in the queue is set to the minimum priority of any edge in the low-level queue of that vertex. If edges are added to (or removed from) the low-level queue, the priority of the corresponding vertex in the mid-level queue may change. If the low-level queue of a vertex is empty, that vertex has priority Inf in the mid-level queue.

At the highest level, unlabeled top-level blossoms are tracked in one global priority queue. The priority of each blossom in this queue is set to the minimum slack of any edge from that blossom to an S-vertex plus Δ. These priorities are invariant under delta steps.

To compute δ₂, we find the minimum priority in the high-level queue and adjust it by Δ. To find the edge associated with δ₂, we use the high-level queue to find the unlabeled blossom with minimum priority, then use that blossom's mid-level queue to find the vertex with minimum priority, then use that vertex's low-level queue to find the edge with minimum priority.

The whole thing is a bit tricky, but it works.

Re-using alternating trees

According to 5, labels and alternating trees should be erased at the end of each stage. However, the algorithm can be optimized by keeping some of the labels and re-using them in the next stage. The optimized algorithm erases only the two alternating trees that are part of the augmenting path. All blossoms in those two trees lose their labels and become free blossoms again. Other alternating trees, which are not involved in the augmenting path, are preserved into the next stage, and so are the labels on the blossoms in those trees.

This optimization is well known and is described for example in [7]. It does not affect the worst-case asymptotic run time of the algorithm, but it provides a significant practical speed up for many types of graphs.

Erasing alternating trees is easy enough, but selectively stripping labels off blossoms has a few implications. The blossoms that lose their labels need to have their modified dual values updated. The T-blossoms additionally need to have their offset_B variables updated to keep the vertex dual values consistent. For S-blossoms that lose their labels, the modified vertex dual variables are updated directly.

The various priority queues also need updating. Former T-blossoms must be removed from the priority queue for δ₄. Edges incident on former S-vertices must be removed from the priority queue for δ₃. Finally, S-vertices that become unlabeled need to construct a proper priority queue of incident edges to other S-vertices for δ₂ tracking. This involves visiting every incident edge of every vertex in each S-blossom that loses its label.

Run time of the algorithm

Every stage of the algorithm either increases the number of matched vertices by 2 or ends the matching. Therefore the number of stages is at most n/2. Every stage runs in O((n + m) log n) steps, therefore the complete algorithm runs in O(n (n + m) log n) steps.

Creating a blossom reduces the number of top-level blossoms by at least 2, thus limiting the number of simultaneously existing blossoms to O(n). Blossoms that are created during a stage become S-blossoms and survive until the end of that stage, therefore O(n) blossoms are created during a stage. Creating a blossom with k sub-blossoms reduces the number of top-level blossoms by k-1, thus limiting the total number of sub-blossoms that can be involved in blossom creation during a stage to O(n).

Creating a blossom involves tracing the alternating path to the closest common ancestor, which takes time O(k log n) for a blossom with k sub-blossoms. It also involves bookkeeping per sub-blossom, which takes time O(log n) per sub-blossom. It also involves relabeling former T-vertices as S-vertices, but I account for that time separately below so I can ignore it here. It also involves merging the concatenable queues which track the vertices in top-level blossoms. Merging two queues takes time O(log n), therefore merging the queues of all sub-blossoms takes time O(k log n). Creating a blossom thus takes time O(k log n). Blossom creation thus takes total time O(n log n) per stage.

During each stage, a blossom becomes an S-blossom or T-blossom at most once. A blossom also becomes unlabeled at most once, at the end of the stage. Changing the label of a blossom takes some simple bookkeeping, as well as operations on priority queues (δ₄ for T-blossoms, δ₂ for unlabeled blossoms) which take time O(log n) per blossom. Assigning label S or removing label S also involves some work per vertex in the blossom, but I account for that time separately below so I can ignore it here. Blossom labeling thus takes total time O(n log n) per stage.

During each stage, an vertex becomes an S-vertex at most once, and an S-vertex becomes unlabeled at most once. In both cases, the incident edges of the affected vertex are scanned and potentially added to or removed from priority queues. This involves finding the top-level blossoms of the endpoints of each edge, which takes time O(log n) per edge. The updates to priority queues also take time O(log n) per edge. Edge scanning thus takes total time O(m log n) per stage.

Note that m ≤ n² therefore log m ≤ 2 log n. This implies that an operation on a priority queue with m elements takes time O(log n).

Expanding a blossom involves some bookkeeping which takes time O(log n) per sub-blossom. It also involves splitting the concatenable queue that tracks the vertices in top-level blossoms, which takes time O(log n) per sub-blossom. In case of a T-blossom, it also involves reconstructing the alternating path through the blossom which takes time O(k log n) for k sub-blossoms. Also in case of a T-blossom, some sub-blossoms will become S-blossoms and their vertices become S-vertices, but I have already accounted for that cost above so I can ignore it here. Expanding a blossom thus takes time O(k log n). The number of blossom expansions during a stage is O(n). Blossom expansion thus takes total time O(n log n) per stage.

The length of an augmenting path is O(n). Tracing the augmenting path and augmenting the matching along the path can be done in O(n log n) steps. Augmenting through a blossom takes a number of steps that is proportional to the number of its sub-blossoms. Since there are fewer than n non-trivial blossoms, the total cost of augmenting through blossoms is O(n) steps. Augmenting thus takes total time O(n log n) per stage.

A delta step limited by δ₁ ends the algorithm and therefore happens at most once. A δ₂ step assigns a label to a previously unlabeled blossom and therefore happens O(n) times per stage. A δ₃ step either creates a blossom or finds an augmenting path and therefore happens O(n) times per stage. A δ₄ step expands a blossom and therefore happens O(n) times per stage. Therefore the number of delta steps is O(n) per stage.

Calculating δ₁ takes constant time. Calculating δ₂ and δ₄ requires a constant number of lookups in priority queues which takes time O(log n) per delta step. During calculation of δ₃, it may be necessary to remove stage edges from the priority queue. Since every edge is inserted into the priority queue at most once per stage, at most O(m) edges are removed per stage, which takes total time O(m log n) per stage. Calculation of δ thus takes total time O((n + m) log n) per stage.

Applying updates to dual variables is done in a lazy fashion as discussed above. The only variable that is updated directly is Δ, which takes time O(1) per delta step. Updating dual variables thus takes total time O(n) per stage.

Implementation details

This section describes some choices I made while implementing the algorithm. There may be easier or faster or better ways to do it, but this is what I did and it seems to work mostly okay.

Data structures

Input graph

Vertices are represented as non-negative integers in range 0 to n-1.

Edges are represented as an array of tuples (x, y, w) where x and y are indices of the incident vertices, and w is the numerical weight of the edge. The edges are listed in no particular order. Each edge has an index in e range 0 to m-1.

edges[e] = (x, y, w)

In addition, edges are organized in an array of adjacency lists, indexed by vertex index. Each adjacency list contains the edge indices of all edges incident on a specific vertex. Every edge therefore appears in two adjacency lists.

adjacent_edges[x] = [e1, e2, ...]

These data structures are initialized at the start of the matching algorithm and never change while the algorithm runs.

Priority queue

Priority queues are used for a number of purposes:

• a priority queue to find the least-slack edge between S-blossoms;
• a priority queue to find the minimum-dual T-blossom;
• a priority queue to find the unlabeled blossom with least-slack edge to an S-blossom;
• a separate priority queue per vertex to find the least-slack edge between that vertex and any S-vertex.

This type of queue is implemented as a binary heap. It supports the following operations:

• insert a new element with specified priority in time O(log n);
• find the element with minimum priority in time O(1);
• delete a specified element in time O(log n);
• change the priority of a specified element in time O(log n).

Concatenable priority queue

Each top-level blossom maintains a concatenable priority queue containing its vertices. We use a specific type of concatenable queue that supports the following operations [4] [5]:

• create a new queue containing 1 new element;
• find the element with minimum priority in time O(1);
• change the priority of a given element;
• merge two queues into one new queue in time O(log n);
• split a queue, thus undoing the previous merge step in time O(log n).

The efficient merge and split operations make it possible to adapt the queue during blossom creation and blossom expansion steps. The priorities in the queue are used to find, for a given top-level blossom, its vertex with least-slack edge to an S-blossom.

The concatenable queue is implemented as a balanced tree, specifically a 2-3 tree. Each internal node of a 2-3 tree has either 2 or 3 children. The leaf nodes of the tree represent the elements of the queue. All leaf nodes are at the same distance from the root. Each node has a pointer to its parent, and each internal node has pointers to its children. Each internal node also stores its height (distance to its leaf nodes).

Only leaf nodes have a priority. However, each internal node maintains a pointer to the leaf node with minimum priority within its subtree. As a consequence, the root of the tree has a pointer to the element with minimum priority. To keep this information consistent, any change in the priority of a leaf node must be followed by updating the internal nodes along a path from the leaf node to the root. The same must be done when the structure of the tree is adjusted.

The left-to-right order of the leaf nodes is preserved during all operations, including merge and split. When trees A and B are merged, the sequence of leaf nodes in the merged tree will consist of the leaf nodes A followed by the leaf nodes of B. Note that the left-to-right order of the leaf nodes is unrelated to the priorities of the elements.

To merge two trees, the root of the smaller tree is inserted as a child of an appropriate node in the larger tree. Subsequent adjustments are needed restore the consistency the 2-3 tree and to update the minimum-element pointers of the internal nodes along a path from the insertion point to the root of the merged tree. This can be done in a number of steps proportional to the difference in height between the two trees, which is in any case O(log n).

To split a tree, a split node is identified: the left-most leaf node that must end up in the right-side tree after splitting. Internal nodes are deleted along the path from the split node to the root of the tree. This creates a forest of disconnected subtrees on the left side of the path, and a similar forest of subtrees on the right side of the split path. The left-side subtrees are reassembled into a single tree through a series of merge steps. Although O(log n) merge steps may be needed, the total time required for reassembly is also O(log n) because each merge step combines trees of similar height. A similar reassembly is done for the forest on the right side of the split path.

The concatenable queues have an additional purpose in the matching algorithm: finding the top-level blossom that contains a given vertex. To do this, we assign a name to each concatenable queue instance, which is simply a pointer to the top-level blossom that maintains the queue. An extra operation is defined: find the name of the queue instance that contains a given element in time O(log n).

Implementing the find operation is easy: Starting at the leaf node that represents the element, follow parent pointers to the root of the tree. The root node contains the name of the queue.

General data

vertex_mate[x] = y if the edge between vertex x and vertex y is matched.
vertex_mate[x] = -1 if vertex x is unmatched.

vertex_dual[x] holds the modified vertex dual u'_x.

A global list holds vertex indices of S-vertices whose edges have not yet been scanned. Vertices are inserted in this list when their top-level blossom gets label S.

Blossoms

A blossom is either a single vertex or a non-trivial blossom. Both types of blossoms are represented as class instances with the following attributes:

• B.base_vertex is the vertex index of the base vertex of blossom B.
• B.parent is a pointer to the parent of B in the blossom structure tree, or None if B is a top-level blossom.
• B.label is S or T or None
• B.tree_edge = (x, y) if B is a labeled top-level blossom, where y is a vertex in B and (x, y) is the edge that links B to its parent in the alternating tree.
• B.tree_blossoms points to a list of blossoms in the same alternating tree, if B is a labeled top-level blossom.
• B.vertex_dual_offset holds the pending change to vertex duals offset_B.

A non-trivial blossom additionally has the following attributes:

• B.subblossoms is an array of pointers to the sub-blossoms of B, starting with the sub-blossom that contains the base vertex.
• B.edges is an array of alternating edges connecting the sub-blossoms.
• B.dual_var holds the modified blossom dual z'_B.

Single-vertex blossoms are kept in an array indexed by vertex index.
Non-trivial blossoms are kept in a separate list.
These arrays are used to iterate over blossoms and to find the trivial blossom that consists of a given vertex.

Memory usage

The data structures described above use a constant amount of memory per vertex and per edge and per blossom. Therefore the total memory requirement is O(m + n).

Recursion

Certain tasks in the algorithm are recursive in nature: enumerating the vertices in a given blossom, and augmenting the matching along a path through a blossom. It seems natural to implement such tasks as recursive subroutines, which handle the task for a given blossom and make recursive calls to handle sub-blossoms as necessary. But the recursion depth of such implementations can grow to O(n) in case of deeply nested blossoms.

Deep recursion may cause problems in certain programming languages and runtime environments. In such cases, it may be better to avoid recursive calls and instead implement an iterative control flow with an explicit stack.

Handling integer edge weights

If all edge weights in the input graph are integers, it is possible and often desirable to implement the algorithm such that only integer calculations are used.

If all edge weights are integers, then all vertex dual variables u_x are integer multiples of 0.5, and all blossom dual variables z_B are integers. Storing the vertex duals as 2*u_x allows all calculations to be done with integers.

Proof by induction that all vertex duals are multiples of 0.5 and all blossom duals are integers:

• Vertex duals are initialized to 0.5 times the greatest edge weight. Blossom duals are initialized to 0. Therefore the proposition is initially true.
• All unmatched vertices have the same dual value. Proof: Initially all vertices have the same dual value. All unmatched vertices have been unmatched since the beginning, therefore always had label S in every dual variable update, therefore always got changed by the same amount.
• Either all duals of S-vertices are integers or all duals of S-vertices are odd multiples of 0.5. Proof: The root nodes of alternating trees are unmatched vertices which all have the same dual. Within an alternating tree, all edges are tight, therefore all duals of vertices in the tree differ by an integer amount, therefore either all duals are integers or all duals are odd multiples of 0.5.
• δ is a multiple of 0.5. Proof:
  • δ₁ = u_x and u_x is a multiple of 0.5, therefore δ₁ is a mutiple of 0.5.
  • δ₂ = π_x,y = u_x + u_y - w_x,y where u_x and u_y and w_x,y are multiples of 0.5, therefore δ₂ is a multiple of 0.5.
  • δ₃ = 0.5 * π_x,y = 0.5 * (u_x + u_y - w_x,y). Since x and y are S-vertices, either u_x and u_y are both integers or both are odd multiples of 0.5. In either case u_x + u_y is an integer. Therefore δ₃ is a multiple of 0.5.
  • δ₄ = 0.5 * z_B where z_B is an integer, therefore δ₄ is a multiple of 0.5.
• Vertex duals increase or decrease by δ which is a multiple of 0.5, therefore updated vertex duals are still multiples of 0.5.
• Blossom duals increase or decrease by 2*δ, therefore updated blossom duals are still integers.

It is useful to know that (modified) dual variables and (modified) edge slacks are limited to a finite range of values which depends on the maximum edge weight. This may be helpful when choosing an integer data type for these variables. (Alternatively, choose a programming language with unlimited integer range. This is perhaps the thing I love most about Python.)

• The value of Δ (sum over δ steps) does not exceed maxweight / 2. Proof:
  • Vertex dual variables start at u_x = maxweight / 2.
  • While the algorithm runs, there is at least one vertex which has been unmatched since the beginning. This vertex has always had label S, therefore its dual is maxweight/2 - Δ. Vertex deltas can not be negative, therefore Δ ≤ maxweight/2.
• Vertex duals are limited to the range 0 to maxweight.
• Blossom duals are limited to the range 0 to maxweight.
• Edge slack is limited to the range 0 to 2*maxweight.
• Modified vertex duals are limited to the range 0 to 1.5*maxweight.
• Modified blossom duals are limited to the range -maxweight to 2*maxweight.
• Modified edge slack is limited to the range 0 to 3*maxweight.
• Dual offsets are limited to the range -maxweight/2 to maxweight/2.

Handling floating point edge weights

Floating point calculations are subject to rounding errors. As a result, the algorithm may return a matching which has slightly lower weight than the actual maximum weight.

I believe the matching algorithm is stable for floating point weights. It seems to me that the algorithm will always return a matching that is close to optimal, and could have been optimal if the edge weights were changed by very small amounts. I must admit this is mostly based on intuition. Unfortunately I don't know how to properly analyze the floating point accuracy of this algorithm.

The most challenging cases are probably graphs where edge weights differ by many orders of magnitude.

Finding a maximum weight matching out of all maximum cardinality matchings

It is sometimes useful to find a maximum cardinality matching which has maximum weight out of all maximum cardinality matchings. A simple way to achieve this is to increase the weight of all edges by the same amount.

In general, a maximum weight matching is not necessarily a maximum cardinality matching. However if all edge weights are at least n times the difference between the maximum and minimum edge weight, any maximum weight matching is guaranteed to have maximum cardinality. Proof: The weight of a non-maximum-cardinality matching can be increased by matching an additional edge. In order to match that extra edge, some high-weight edges may have to be removed from the matching. Their place might be taken low-weight edges. But even if all previously matched edges had maximum weight, and all newly matched edges have minimum weight, the weight of the matching will still increase.

Changing all edge weights by the same amount does not change the relative preference for a certain groups of edges over another group of the same size. Therefore, given that we only consider maximum-cardinality matchings, changing all weights by the same amount doesn't change which of these matchings has maximum weight.

References

1. Jack Edmonds, "Paths, trees, and flowers." Canadian Journal of Mathematics vol. 17 no. 3, 1965. (link) (pdf)

2. Jack Edmonds, "Maximum matching and a polyhedron with 0,1-vertices." Journal of research of the National Bureau of Standards vol. 69B, 1965. (pdf)

3. Harold N. Gabow, "Implementation of algorithms for maximum matching on nonbipartite graphs." Ph.D. thesis, Stanford University, 1974.

4. Z. Galil, S. Micali, H. Gabow, "An O(EV log V) algorithm for finding a maximal weighted matching in general graphs." SIAM Journal on Computing vol. 15 no. 1, 1986. (link) (pdf)

5. Zvi Galil, "Efficient algorithms for finding maximum matching in graphs." ACM Computing Surveys vol. 18 no. 1, 1986. (link) (pdf)

6. Harold N. Gabow, "Data structures for weighted matching and nearest common ancestors with linking." Proc. 1st ACM-SIAM symposium on discrete algorithms, 1990. (link) (pdf)

7. Kurt Mehlhorn, Guido Schäfer, "Implementation of O(nm log(n)) Weighted Matchings in General Graphs: The Power of Data Structures", Journal of Experimental Algorithmics vol. 7, 2002. (link) (pdf)

8. Alfred V. Aho, John E. Hopcroft, Jeffrey D. Ullman, The Design and Analysis of Computer Algorithms, Addison-Wesley, 1974.

---

Written in 2023-2024 by Joris van Rantwijk. This work is licensed under CC BY-ND 4.0.